一、公钥技术现状

在非对称密码系统中，一个用户有两把钥匙：一把公开，另一把为用户私有。这类密码系统需要解决一个关键问题：各个用户如何安全地公开自己的公钥而不引起混乱或安全性风险，简单地讲就是如何将用户的身份和用户的钥匙对应起来。为了应对公钥密码机制面临的中间人替换公钥攻击的风险，目前有三类主要的解决方案。

第一种方案是采用证书机制实现用户的身份和用户的钥匙之间的安全对应。证书机制一般都采用公钥基础设施（Public Key Infrastructure: PKI）技术。它综合使用了数字摘要技术、数字签名等密码技术以及一套完整的证书管理机制来提供安全服务。系统建设有公信力的认证中心（Certification Authority：CA）鉴定用户身份，然后为用户签发数字证书。数字证书安全地将用户身份和用户密钥绑定在一起。用户在业务系统中先交换证书，然后使用公私钥完成用户的身份认证、访问控制、信息安全传递等操作。但加密操作过程中数据发送方需要预先获得接收方证书，进而获取加密公钥，相关过程较为复杂。因此，目前证书系统广泛用于提供数字签名服务，实现身份认证、数据一致性保护等。为了进一步降低证书管理的复杂性，目前还有一些轻量级的证书管理协议，如简单证书注册协议SCEP等来降低证书注册等流程的复杂性。

第二种方案是基于标识的密码技术 (Identity-Based Cryptography：IBC)。为了降低公钥系统中密钥管理和使用的复杂性，Shamir在1984年提出了基于标识的密码机制。在这种系统中，用户的标识就可以用做用户的公钥（更加准确地说是用户的公钥可以从用户的标识和标识密码算法规定的一个方法计算得出）。在这种情况下，用户不需要申请和交换证书，而是直接使用标识进行密码运算，从而解决公钥真实性问题，极大地简化了密钥系统管理的复杂性。这类系统中用户的私钥由系统中的一受信任的第三方（密钥生成中心：KGC）使用标识私钥生成算法计算生成。这样的系统具有天然的密码委托功能，特别适合于对数据恢复有需求的应用环境。另外这类基于标识的密码系统相较于传统PKI具有巨大的灵活性、扩展性、简洁性。因为系统加密过程直接使用应用涉及的标识作为公钥，无需分发、查询证书、无需申请策略证书等，充分体现了加密操作的便捷性。应用系统涉及的标识只要具有唯一性特征就可以直接作为公钥进行密码应用。这些标识可以具有任意的格式、属性，可以是常用的用户标识如邮件地址、手机号码、身份证号码；在物联网中可以是设备标识、Handle码、OID等；还可以是数据安全控制策略的形式化编码、生物特征信息、甚至是标识属性集等，特别适合基于标识、基于属性的权限访问控制和数据安全保护。在密码运算中直接使用这类标识作为公钥运算，无需进行证书申请、无需额外的实体标识与公钥间的映射管理，充分体现了标识密钥的灵活性。

第三种方案是无证书的密码体制。该体制的代表有1991年Girault 提出的“隐式证书”密码系统(Implicit Certificate)和Al-Riyami和Paterson在2001年提出的无证书公钥密码体制（AP-CL-PKC）。这种密码体制介于传统PKI和标识密码技术之间。这种机制中用户私钥由两个秘密因素决定：一个是从密钥生成中心中提取的与用户身份相关的密钥，另一个是由用户自己生成的密钥。从一个秘密元素不能计算另一个，即密钥生成中心不能算出用户的部分密钥，用户也算不出密钥生成中心生成的部分密钥。 因此，无证书密码系统没有密钥托管的功能。无证书密码系统保证即使是攻击人成功地用自己的公钥代替了受害者的公钥，攻击人仍然无法伪造一个受害者的签名，或者解密一段加密给受害者的密文信息。这一点无疑会减少恶意攻击者的兴趣。这种密码机制在加密过程中仍然提前需要获取接收方公钥（实际为公钥还原数据），然后使用接收方标识和系统参数计算接收方完整公钥。因此这类密码系统在加密应用中面临传统PKI类似的挑战，即需要预先获得接收方的公钥还原数据。对于签名过程，签名方可以将其公钥还原数据作为签名的一部分一起传递，验签方从签名结果中提取签名人的公钥还原数据，然后使用签名方标识和系统参数计算签名方的完整公钥，验证签名的正确性。因此这类系统在签名应用中具有无证书管理、系统轻量、通信开销低、具有强不可抵赖性等众多优点，非常适合物联网等领域的身份认证应用。

“隐式证书”密码系统和Al-Riyami-Paterson无证书密码体系经过三十年的发展，仍然面临包括统一安全模型、基于标准算法的算法安全构造等一系列问题。

（一）隐式证书密码系统

隐式证书密码系统是由Girault在1991年提出的自认证公钥机制发展起来的。隐式证书系统中用户生成部分公钥，再把这部分公钥和用户标识提交到系统中的密钥生成中心（KGC）进行签名。这一过程类似于CA中心签发证书，但是KGC计算生成的是用户的公钥还原数据和部分私钥，而非签发的证书。用户的完整公钥是由用户的标识、公钥还原数据、KGC的主公钥通过指定的算法计算得出。隐式证书的优势是上述过程（本文通称为密钥生成算法）生成的用户私钥和还原的用户公钥和标准RSA、ECC算法的密钥对形式相同，因此理论上可以结合标准算法进行使用。比如Petersenl和Horster在1997提出基于Schnorr签名算法生成的密钥对可结合标准ECC算法进行应用。遗憾的是这种简单的组合并不能保证完整密码系统的安全性。比如Petersenl-Horster的密钥生成算法和ECDSA结合应用时完全不能抵抗伪造签名攻击。1998年Arazi提出基于Schnorr签名算法变形的密钥生成算法。这个方法后来发展成为ECQV。ECQV结合ECDSA可以抵抗众多攻击，但仍然不能抵抗对特定消息的伪造签名攻击。隐式证书密码系统一直没有严格的安全性模型，构造的算法均采用启发式方法进行分析，没有严格的安全性证明，因此出现密码系统被发现存在攻击的现象。

（二）Al-Riyami-Paterson无证书公钥系统

Al-Riyami和Paterson在2001年提出无证书的密码体制后引起广泛的关注。学术界进行了大量的安全模型理论研究并构造了一系列包括无证书加密算法、签名算法和密钥交换协议等安全机制。遗憾的是，由于Al-Riyami和Paterson对CL-PKC中密钥生成算法的定义方法导致这类模型无法覆盖隐式证书系统，生成的密钥对难以结合标准的如ECC密码算法使用。一些基于标准算法的无证书签名算法构造都被证明不能满足 Al-Riyami和Paterson的安全模型。下面简单描述AP-CL-PKC中的密钥生成方法（CL-KGA），并分析其局限性。AP-CL-PKC由以下五个函数构成：

其中CL.Gen和CL.Partial-Private-Key-Extract由KGC执行，其他函数由用户执行。用户的完整私钥是sA，用户对外声称其公钥为PA。上述形式化定义有以下局限性：

. CL.Set-Public-Key(Mpt, xA)：用户发布的公钥PA只能由用户生成，无法加入KGC的相关输入。

. CL.Partial-Private-Key-Extract(Mpt, Mst, IDA) ：KGC生成部分私钥的过程只能使用用户的标识，无法灵活使用用户生成的公钥PA。

. Al-Riyami-Paterson在2005年提出将PA作为ID的一部分构造Certificate-Based-Encryption，但是PA在CL.Partial-Private-Key-Extract中仍然不可单独使用。

显然上述定义不能描述隐式证书的生成过程。

二、统一的无证书公钥系统模型

隐式证书具有和标准密码算法结合使用的可能，但是其安全性没有保障。AP-CL-PKC的安全性模型定义非常严格，但是其密钥生成函数的定义排除了隐式证书类的密钥生成方法。我们下面构建统一的无证书公钥系统模型和安全定义来将这两个原来不相容的无证书密码体制统一起来，并同时获得两种机制的优点，从而避免各自的缺点：构建基于标准算法的、安全性可严格证明的无证书密码机制。首先我们定义新的无证书密钥生成算法：

可以看到与AP-CL-PKC中定义不同，CL.Set-User-Key支持额外输出UA，CL.Extract-Partial-Key支持额外输入UA，CL.Set-Public-Key不再使用xA做输入，而需要UA、WA。另外增加CL.Calculate-Public-Key函数计算公钥OA，CL.Verify-Key(Mpt, IDA, PA, sA)可以校验IDA, PA, sA在KGC的系统公钥Mpt下是否正确。

基于以上函数定义我们可以进一步定义密钥生成算法、无证书签名算法、加密算法等的安全模型。这些安全模型的定义采用AP-CL-PKC的定义方法对应两类不同的攻击人：类型-I攻击人是普通的攻击人，他试图冒充他人获得私钥、伪造签名或者获取密文相关信息。类型-II攻击人是好奇的KGC。这类KGC试图在不留痕迹的情况下冒充某个用户获得私钥、伪造签名或者获取密文相关信息。简单描述如下：

三、无证书签名算法的安全构造

下面是介绍基于标准算法ECDSA和SM2构造的无证书签名算法。首先描述密钥生成算法，其中←R表示从集合中随机选取。

（一）CL-KGA算法

（二） 通用无证书签名算法构造方法

为了安全地构造无证书签名算法，这里采用密钥前缀方法，即在计算待签名消息的哈希时将用户的公钥或替代值（如λ或Z||PA）一起进行哈希。此方法能够将无证书密钥生成算法和ECDSA、SM2等签名算法连接在一起形成一个安全、高效的无证书数字签名算法。基本原理如下：

. 哈希算法安全性保证确定的系统公钥和指定的密钥前缀计算指定的签名公钥；

. 前缀化消息(λ||m)强制签名伪造者预先选定签名公；

. 标准签名算法的安全性保证在选定公钥的情况下，无私钥则无法伪造签名；

. 安全的CL-KGA保证没有KGC的帮助，攻击人无法获得选定公钥的私钥。

需要指出的是在这个密钥前缀化过程中，我们对ECDSA、SM2的签名、验签过程是没有任何改变的，因此无需对现有的ECDSA、SM2算法的软、硬件实现进行任何修改。下面分别描述基于λ为密钥前缀基于ECDSA的无证书签名算法，以及以Z||PA为密钥前缀基于SM2的无证书签名算法。

（三）基于ECDSA的无证书签名算法

（四） 基于SM2的无证书签名算法

四、无证书签名算法的实现与应用

前述的无证书签名算法具有广泛的应用场景。所有基于证书的数字签名应用均可以采用这样的算法。这类密码系统相较于基于CA的密码系统，其性能更高：ECC证书的校验需要两个点乘运算，上述公钥计算过程只需要一个点乘，且该点乘可以预计算。证书包括用户的标识、用户的公钥以及CA的签名信息。SM2、ECDSA等采用256比特曲线时签名有64字节。因此无证书的签名算法至少可以节约64字节数据的传递、存储等。下面介绍无证书签名算法在物联网芯片上的实现和车联网中的应用。

（一）通用物联网安全芯片应用

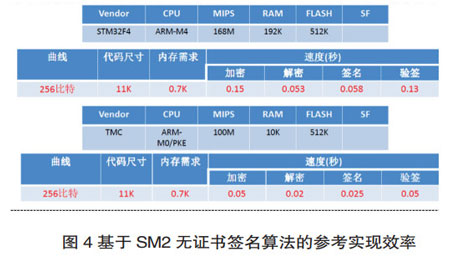
图4是基于SM2的无证书签名在ARM4芯片上的参考实现以及在一高安全芯片上实现的性能报告。ARM-M4上的实现经过汇编优化后整体性能可提高10倍以上，能满足多场景的需求。在高安全芯片上基于芯片内SM2算法和点乘计算硬件，可以高效实现无证书算法。

（二）车联网安全应用

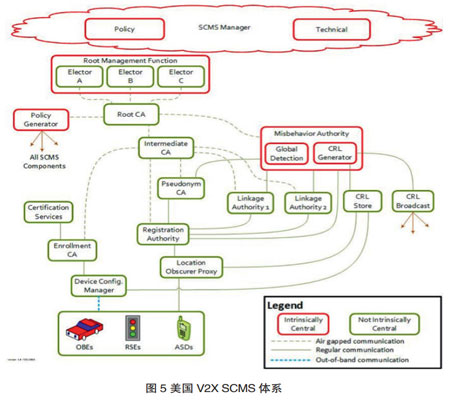
美国的车联网的安全体系SCMS是一个传统的CA体系+无证书密码体制相结合的系统（如图5）。系统中的匿名CA系统并不签发证书，而是采用ECQV算法生成部分私钥和公钥还原数据（隐式证书）。生成的密钥结合ECDSA算法对广播信令消息进行数字签名实现信令消息的数据源认证和一致性保护。该体系设计每年签发3000亿把钥匙。我们设计的基于ECDSA的无证书数字签名算法比ECQV+ECDSA的安全性更好，公钥计算效率更高。

另外2019年，我们推出了基于区块链的无证书密码体系应用。因算法的简洁性和高效性，采用无证书数字签名算法后区块链系统的性能显著提高。目前，我们正在与华为一起推出在TLS协议中集成无证书密码体制的相关标准；在车联网领域，美国相关研究机构已经提出使用我们的算法改进美国V2X系统安全性和性能的方案。

结论

本文描述了统一隐式证书密码系统和Al-Riyami-Paterson无证书密码体系两类无证密码系统的算法定义和安全模型，并采用密钥前缀方法基于标准算法ECDSA、SM2构造了安全性可证明的无证书签名算法。构建的算法可以在现有标准算法的软硬件上快速部署，具有成本低、效率高、安全性好等优势，在物联网、车联网、区块链等领域具有广泛的应用前景。